What’s an Eigenvector and Eigenvalue?

Linear algebra is a cornerstone of many superior mathematical ideas and is extensively utilized in information science, machine studying, laptop imaginative and prescient, and engineering. One of many elementary ideas in linear algebra is eigenvectors, usually paired with eigenvalues. However what precisely is an eigenvector, and why is it so essential?

This text breaks down the idea of eigenvectors in a easy and intuitive method, making it straightforward for anybody to know.

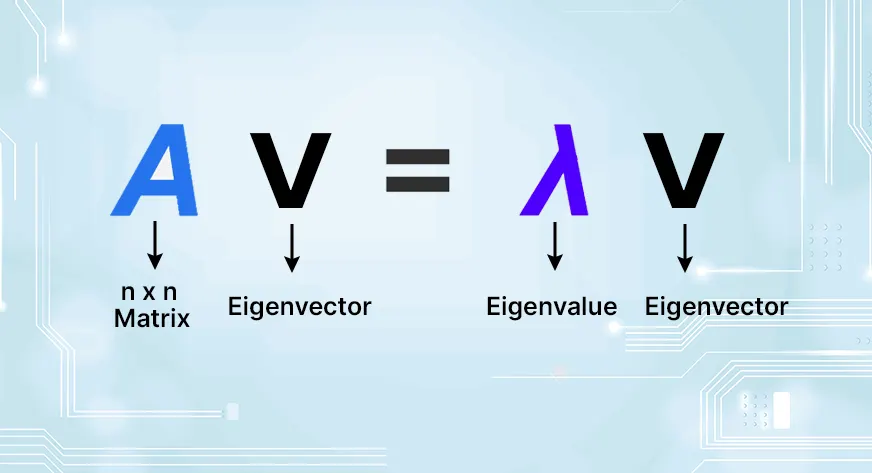
What’s an Eigenvector?

A sq. matrix is associates with a particular kind of vector referred to as an eigenvector. When the matrix acts on the eigenvector, it retains the route of the eigenvector unchanged and solely scales it by a scalar worth referred to as the eigenvalue.

In mathematical phrases, for a sq. matrix A, a non-zero vector v is an eigenvector if:

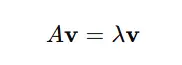
Right here:

• A is the matrix.
• v is the eigenvector.
• λ is the eigenvalue (a scalar).

Instinct Behind Eigenvectors

Think about you will have a matrix A representing a linear transformation, similar to stretching, rotating, or scaling a 2D area. When this transformation is utilized to a vector v:

• Most vectors will change their route and magnitude.
• Some particular vectors, nonetheless, will solely be scaled however not rotated or flipped. These particular vectors are eigenvectors.

For instance:

• If λ>1, the eigenvector is stretched.
• If 0<λ<1, the eigenvector is compressed.
• If λ=−1, the eigenvector flips its route however maintains the identical size.

Why Are Eigenvectors Necessary?

Eigenvectors play an important function in numerous mathematical and real-world functions:

1. Principal Part Evaluation (PCA): PCA is a extensively used approach for dimensionality discount. Eigenvectors are used to find out the principal elements of the information, which seize the utmost variance and assist determine a very powerful options.
2. Google PageRank: The algorithm that ranks internet pages makes use of eigenvectors of a matrix representing the hyperlinks between internet pages. The principal eigenvector helps decide the relative significance of every web page.
3. Quantum Mechanics: In physics, eigenvectors and eigenvalues describe the states of a system and their measurable properties, similar to vitality ranges.
4. Laptop Imaginative and prescient: Eigenvectors are utilized in facial recognition methods, significantly in strategies like Eigenfaces, the place they assist characterize photographs as linear mixtures of serious options.
5. Vibrational Evaluation: In engineering, eigenvectors describe the modes of vibration in buildings like bridges and buildings.

Easy methods to Compute Eigenvectors?

To search out eigenvectors, observe these steps:

• Arrange the eigenvalue equation: Begin with Av=λv and rewrite it as (A−λI)v=0, the place I is the identification matrix. Clear up for eigenvalues: Discover eigenvectors:
• Clear up for eigenvalues: Compute det⁡(A−λI)=0 to seek out the eigenvalues λ.
• Discover eigenvectors: Substitute every eigenvalue λ into (A−λI)v=0 and resolve for v.

Instance: Eigenvectors in Motion

Take into account a matrix:

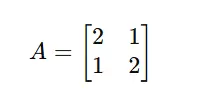
Step 1: Discover eigenvalues λ.

Clear up det⁡(A−λI)=0:

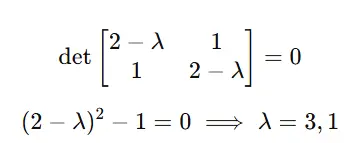
Step 2: Discover eigenvectors for every λ.

For λ=3:

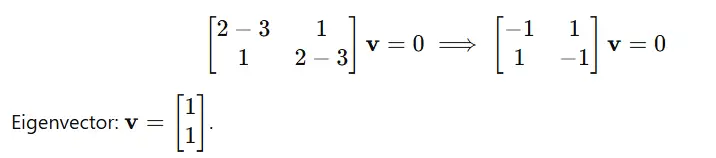
For λ=1:

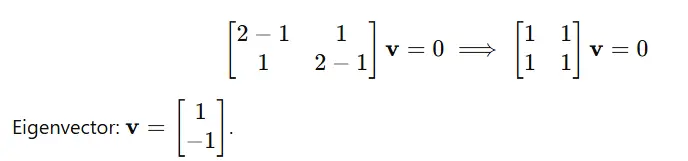
Python Implementation

Let’s compute the eigenvalues and eigenvectors of a matrix utilizing Python.

Instance Matrix

Take into account the matrix:

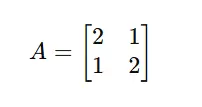
Code Implementation

import numpy as np

# Outline the matrix
A = np.array([[2, 1], [1, 2]])

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)

# Show outcomes
print("Matrix A:")
print(A)

print("nEigenvalues:")
print(eigenvalues)

print("nEigenvectors:")
print(eigenvectors)

Output:

Matrix A:
[[2 1]
 [1 2]]

Eigenvalues:
[3. 1.]

Eigenvectors:
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

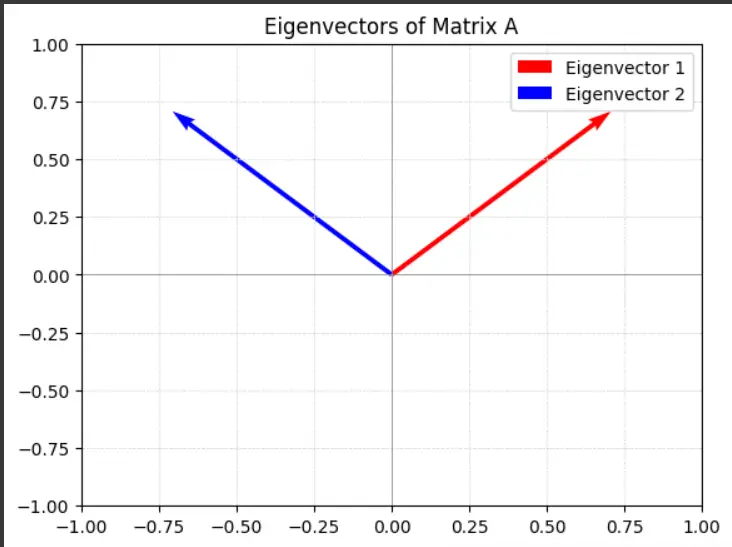
Visualizing Eigenvectors

You may visualize how eigenvectors behave beneath the transformation outlined by matrix A.

Visualization Code

import matplotlib.pyplot as plt

# Outline eigenvectors
eig_vec1 = eigenvectors[:, 0]
eig_vec2 = eigenvectors[:, 1]

# Plot authentic eigenvectors
plt.quiver(0, 0, eig_vec1[0], eig_vec1[1], angles="xy", scale_units="xy", scale=1, colour="r", label="Eigenvector 1")
plt.quiver(0, 0, eig_vec2[0], eig_vec2[1], angles="xy", scale_units="xy", scale=1, colour="b", label="Eigenvector 2")

# Alter plot settings
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.axhline(0, colour="grey", linewidth=0.5)
plt.axvline(0, colour="grey", linewidth=0.5)
plt.grid(colour="lightgray", linestyle="--", linewidth=0.5)
plt.legend()
plt.title("Eigenvectors of Matrix A")
plt.present()

This code will produce a plot displaying the eigenvectors of AAA, illustrating their instructions and the way they continue to be unchanged beneath the transformation.

Key Takeaways

• Eigenvectors are particular vectors that stay in the identical route when remodeled by a matrix.
• They’re paired with eigenvalues, which decide how a lot the eigenvectors are scaled.
• Eigenvectors have important functions in information science, machine studying, engineering, and physics.
• Python offers instruments like NumPy to compute eigenvalues and eigenvectors simply.

Conclusion

Eigenvectors are a cornerstone idea in linear algebra, with far-reaching functions in information science, engineering, physics, and past. They characterize the essence of how a matrix transformation impacts sure particular instructions, making them indispensable in areas like dimensionality discount, picture processing, and vibrational evaluation.

By understanding and computing eigenvectors, you unlock a robust mathematical software that allows you to resolve advanced issues with readability and precision. With Python’s strong libraries like NumPy, exploring eigenvectors turns into easy, permitting you to visualise and apply these ideas in real-world situations.

Whether or not you’re constructing machine studying fashions, analyzing structural dynamics, or diving into quantum mechanics, a stable understanding of eigenvectors is a talent that may serve you effectively in your journey.

Often Requested Questions

Hello, I’m Janvi, a passionate information science fanatic presently working at Analytics Vidhya. My journey into the world of knowledge started with a deep curiosity about how we are able to extract significant insights from advanced datasets.